Context
Carrying on from Phase I, I wanted to see how I could take the initial answer and make it more efficient. The first port of call then is… how expensive is it at the moment. Will any changes I make have a significant impact on that baseline.
timeit
I dont think using %%timeit as an ipython coding secret on the cell will cut the mustard, but we shall see. I would like to be able to single out code sections for timing too.
Calc Pi Unoptimised
def calc_pi(num_attempts, display_plot=False):
import matplotlib
import matplotlib.pyplot as plt
from random import random
inside = 0
x_inside = []
y_inside = []
x_outside = []
y_outside = []
for _ in range(num_attempts):
x = random()
y = random()
if x**2+y**2 <= 1:
inside += 1
x_inside.append(x)
y_inside.append(y)
else:
x_outside.append(x)
y_outside.append(y)
pi = 4*inside/num_attempts
if display_plot:
fig, ax = plt.subplots()
ax.set_aspect('equal')
ax.scatter(x_inside, y_inside, color='g')
ax.scatter(x_outside, y_outside, color='r')
return pi
Calc Pi Quick (Version 1)
Quick Python only changes, remove array recording and if we never plan to plot remove the if statement
def calc_pi_quick(num_attempts: int):
inside = 0
for _ in range(num_attempts):
x = random()
y = random()
if x**2+y**2 <= 1:
inside += 1
return 4*inside/num_attempts
Initial comparison
from timeit import default_timer as timer
from datetime import timedelta
start = timer()
calc_pi(50000000, True)
end = timer()
print(timedelta(seconds=end-start))
start = timer()
calc_pi(50000000, False)
end = timer()
print(timedelta(seconds=end-start))
start = timer()
calc_pi_quick(50000000)
end = timer()
print(timedelta(seconds=end-start))
Output
calc_pi with plotly display time: 0:00:08.318734 calc_pi no display time: 0:00:00.625193 calc_pi_quick time: 0:00:00.470770
We start to see there are some decent performance benefits. Lets check if these are linear or not. However to see some really decent improvements I think we can start to think about threading perhaps? Also if we still wanted to record the hit and miss positions, would numpy be quick enough that we can keep this data without a significant performance hit?
Numpy Optimisation Attempts
Spoiler Alert… my first attempt was absolutely terrible. However, in a way that’s great news. I now know what not to do with numpy on a non trivial problem, and now so do you.
def calc_pi_numpi_bad(num_attempts):
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from random import random
inside = 0
x_inside = np.array([])
y_inside = np.array([])
x_outside = np.array([])
y_outside = np.array([])
for _ in range(num_attempts):
x = random()
y = random()
if x**2+y**2 <= 1:
inside += 1
x_inside = np.append(x_inside, x)
y_inside = np.append(y_inside, y)
else:
x_outside = np.append(x_outside, x)
y_outside = np.append(y_outside, y)
pi = 4*inside/num_attempts
return pi
How bad? Well lets see…
def measure_performance_verbose(num_attempts: int) -> None:
from timeit import default_timer as timer
from datetime import timedelta
start = timer()
calc_pi(num_attempts, False)
end = timer()
time_taken = end-start
print('calc_pi time: {}'.format(timedelta(seconds=time_taken)))
start = timer()
calc_pi_quick(num_attempts)
end = timer()
quick_time_taken = end-start
print('calc_pi_quick time: {}'.format(timedelta(seconds=quick_time_taken)))
percentage_improvement = quick_time_taken / time_taken * 100
print('Precentage improvement: {}'.format(percentage_improvement))
start = timer()
calc_pi_numpi(num_attempts)
end = timer()
numpi_time_taken = end-start
print('calc_pi_numpi time: {}'.format(timedelta(seconds=numpi_time_taken)))
start = timer()
calc_pi_numpi_bad(num_attempts)
end = timer()
numpi_bad_time_taken = end-start
print('calc_pi_numpi_bad time: {}'.format(timedelta(seconds=numpi_bad_time_taken)))
measure_performance_verbose(500_000)
calc_pi time: 0:00:00.636658
calc_pi_quick time: 0:00:00.462309
Precentage improvement: 72.6149660351135
calc_pi_numpi time: 0:00:00.616958
calc_pi_numpi_bad time: 0:12:52.784511
Whoa, what just happened there. It takes TWELVE seconds to run for 500,000 attempts. That is atrocious.
Lets look at the documentation for this function.
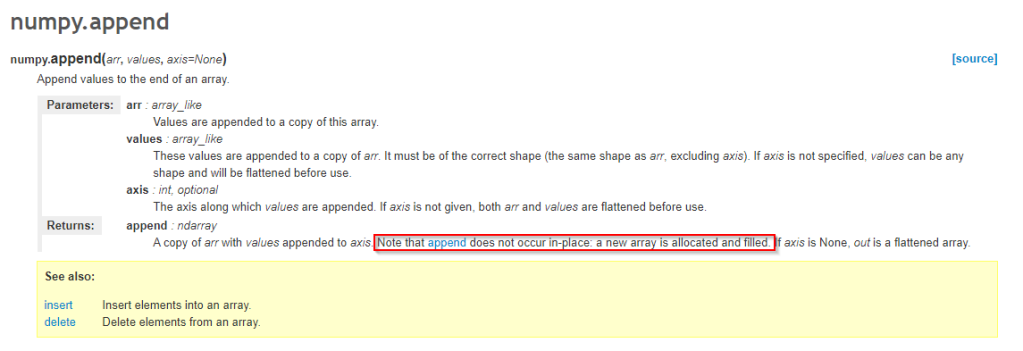
Ahh, that explains it. Every append copies the existing array into a new one. I did not know that, shame on me. I have always used np arrays as data converted from pandas or existing python lists, not created and appended to them on the fly.
However, we can fix it by pre-allocating the mem to the max num required and then mask the results if zero in plotly.
def calc_pi_numpi(num_attempts, display_plot=False, display_masked_plot=False):
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from random import random
inside = 0
x_inside = np.zeros(num_attempts)
y_inside = np.zeros(num_attempts)
x_outside = np.zeros(num_attempts)
y_outside = np.zeros(num_attempts)
for i in range(num_attempts):
x = random()
y = random()
if x**2+y**2 <= 1:
inside += 1
x_inside[i] = x
y_inside[i] = y
else:
x_outside[i] = x
y_outside[i] = y
if display_masked_plot:
fig, ax = plt.subplots()
ax.set_aspect('equal')
ax.scatter(np.ma.masked_equal(x_inside,0), np.ma.masked_equal(y_inside,0), color='g')
ax.scatter(np.ma.masked_equal(x_outside,0), np.ma.masked_equal(y_outside,0), color='r')
if display_plot:
x_inside2 = x_inside[x_inside !=0]
y_inside2 = y_inside[y_inside !=0]
x_outside2 = x_outside[x_outside !=0]
y_outside2 = y_outside[y_outside !=0]
fig, ax = plt.subplots()
ax.set_aspect('equal')
ax.scatter(x_inside2, y_inside2, color='g')
ax.scatter(x_outside2, y_outside2, color='r')
pi = 4*inside/num_attempts
return pi
There are two booleans so that we can test that both work.
calc_pi_numpi(256, True, True)

numpy zero removal
start = timer()
calc_pi_numpi(500_000, True, False)
end = timer()
time_taken = end-start
print('calc_pi normal display time: {}'.format(timedelta(seconds=time_taken)))
start = timer()
calc_pi_numpi(500_000, False, True)
end = timer()
time_taken = end-start
print('calc_pi masked display time: {}'.format(timedelta(seconds=time_taken)))
calc_pi normal display time: 0:00:02.356013 calc_pi masked display time: 0:00:04.012019
Much much better.
start = timer()
calc_pi_numpi(500_000, False, False)
end = timer()
time_taken = end-start
print('calc_pi no display time: {}'.format(timedelta(seconds=time_taken)))
start = timer()
calc_pi(500_000)
end = timer()
time_taken = end-start
print('calc_pi no display time: {}'.format(timedelta(seconds=time_taken)))
calc_pi no display time: 0:00:00.622075 calc_pi no display time: 0:00:00.655379
So… numpy doesn’t make things better, but used correctly, doesn’t make things any worse. So this is a dead end. Also we don’t want to plot for the numbers higher than a million as it looks to the human eye to be , a complete quarter circle. in plotly anyway so we dont need to store large amounts of array data anyway
While I am here I wanted to utilise the “functions are first class objects” paradigm in python. I have hinted at it by showing the initial fuction as _verbose but its much cleaner to call that same code within a functor ( of sorts ) loop as below.
def measure_performance(num_attempts: int) -> None:
from timeit import default_timer as timer
from datetime import timedelta
funcs_to_call = [calc_pi, calc_pi_quick, calc_pi_numpi, calc_pi_numpi_bad]
for func in funcs_to_call:
start = timer()
calc_pi(num_attempts, False)
end = timer()
time_taken = end-start
print('{} time: {}'.format(func.__name__, timedelta(seconds=time_taken)))
measure_performance(50000)
In Phase III -> aka PiMultiCarlo I want to loo at what we can do locally on a decent multi core machine to get some decent speed improvements for only calculating the number only, not storing the guesses.
Follow-up
For Part III : CALCULATE PI USING MONTECARLO SIMULATION – PHASE III – aka “Multicarlo”
